leetcode_二叉树相关题目(1)

2019-02-07

二叉树数据结构里还挺常用的，但是都快忘记了，就来刷一下题回顾一下，顺便还能练练python

二叉树的最大深度

题目

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3

分析

二叉树的深度倒还真记得是什么东西，从示例来看，貌似节点是一层一层铺上去的

解法1—迭代

这种方法，写起来比较省事省心，很精巧，看代码应该看得懂，把每层的节点都当作根节点计算一次，如果读到空就将层数加1后返还

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:
            return 0
        else:
            right_height = self.maxDepth(root.right)
            left_height = self.maxDepth(root.left)
            return max(left_height, right_height) + 1

解法2—DFS

深度遍历算法是个啥其实我已经忘记了233，百度一下

深度优先遍历（DFS）；

1、访问指定的起始顶点；

2、若当前访问的顶点的邻接顶点有未被访问的，则任选一个访问之；反之，退回到最近访问过的顶点；直到与起始顶点相通的全部顶点都访问完毕；

3、若此时图中尚有顶点未被访问，则再选其中一个顶点作为起始顶点并访问之，转 2；反之，遍历结束。

当然这是图的情况，如果是连通图的话就和二叉树有点类似了，一开始用一个list或者dict存储各个节点是否被访问过的状态是不错的选择

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        stack = []
        if root is not None:
            stack.append((1,root))  # 若根节点非空，则压入
        depth = 0
        while stack !=[]:
            current_depth, root = stack.pop()
            if root is not None:
                depth = max(depth, current_depth)
                stack.append((current_depth + 1, root.left))
                stack.append((current_depth + 1, root.right))
        return depth

因为二叉树肯定是连通的，其实就是每个节点不断地向左右衍生直到尽头，这么想像，其实和迭代也是很相似的，只不过他是把所有的深度进行比较，而迭代则是把左右节点中的最大深度选择一个大的

二叉搜索树的最近公共祖先

什么是二叉搜索树

一开始看到这个名字有点懵，查了下概念，逐渐有了印象

二叉搜索树，又称二叉排序树。它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。

题目

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

1
2
3

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

1
2
3

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

分析

好在说明里说了节点是唯一的，也比较贴近生活，生活中完完全全一样的东西肯定还是少的，但肯定也有局限性，统计数字之类就不是很好办，比如考试同分，但这就不满足儿茶搜索树的定义了，反正先把简单的弄懂再说

解题

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if q.val >= root.val >= p.val or q.val <= root.val <=p.val:
            return root
        elif q.val > root.val and p.val > root.val:
            return self.lowestCommonAncestor(root.right,p,q)
        elif q.val < root.val and p.val < root.val:
            return self.lowestCommonAncestor(root.left,p,q)
        else:
            return None

其实理解了最基本的迭代的话还是比较轻松的，目的就是不断地把输入的p，q两个节点放在某一个节点的两侧，达成这个目的就好，函数内部调用自身不要忘记self就好

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

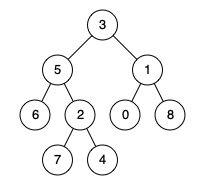
示例 1:

1
2
3

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

1
2
3

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

分析

没有排序，不能无脑迭代了，要稍微想一想，题目难度从简单一下变成了中等，中等难度的，不看答案的话，目前而言我写不出正确以及优雅的代码，难受

解题

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if not root or p == root or q == root:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left == None:
            return right
        if right == None:
            return left
        return root

这个迭代比上一个感觉难理解一些，大概就是遍历，如果返还的左右子树都有值，那么最近公共祖先就在根节点上，但如果有一边的子树没有返回值，那最近祖先就一定在另一边的子树上

本文作者： xiaoyuyu
本文链接： http://woaixiaoyuyu.github.io/2019/02/07/leetcode-%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9B%B8%E5%85%B3%E9%A2%98%E7%9B%AE/
版权声明： 本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。转载请注明出处！